Контрольная работа
Шифр студента 744
Задача №1
Расчет плоской рамы на устойчивость
Задача №2
Динамический расчет плоской системы
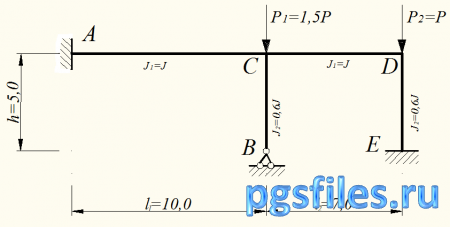
Для статически неопределимой рамы (рис. 1) требуется определить значения критической нагрузки и коэффициент запаса по устойчивости.
Исходные данные:
Ɩ1=10,0м; Ɩ2=7,0м
h=5,0м; J2:J1=0,6;
α=Р1/ Р2=1,5; Номер схемы-№4
Рис. 1
Определяем параметры ν для сжатых стоек:
Определяем количество неизвестных метода перемещений:
n = nу + nл
Рама имеет два жестких узла D и С, поэтому nу=2
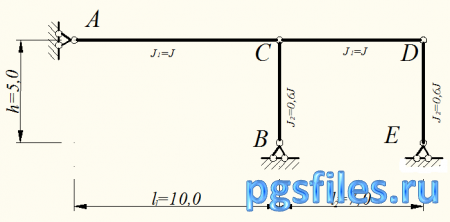
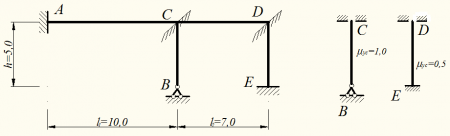
Число линейных перемещений определим по шарнирной схеме, образованной из заданной рамы (см. рис. 2):
Рис. 2
nл = 3D – 2Ш0 - С0 = 3*4 - 2* 3 - 6 = 0
n = nу + nл=2+0=2
Выбираем основную систему метода перемещений, накладывая на узлы D и С связи «1» и «2», препятствующих повороту узлов.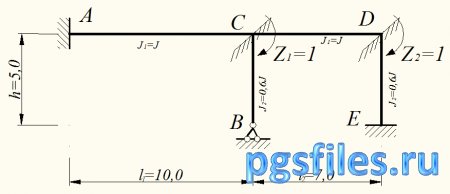
Рис. 3
Записываем систему канонических уравнений метода перемещений:
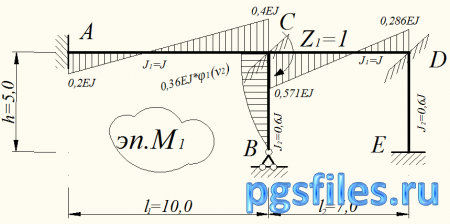
Используя табличные данные справочной литературы построим эпюры моментов от единичных перемещений введенных связей по заданным направлениям.
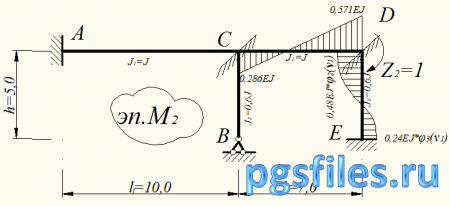
Рис. 4
Рис. 5
Рис. 6
Рис. 7
Составляем выражения для коэффициентов при неизвестных:
- от действия усилия Z1=1
вырезаем узел С:
вырезаем узел D
- от действия усилия Z2=1
вырезаем узел С:
вырезаем узел D
Записываем уравнение устойчивости:
Находим пределы возможного изменения параметра ν. Для упрощения «ослабленную» систему не рассматриваем, а принимаем нижний предел ν=0.
В качестве усиленной схемы принимаем основную систему метода перемещений:
Из двух значений (ν=2,56 и ν=6,28) выбираем меньшее значение νус=2,56.
Таким образом:
0 ≤ ν ≤ 2,56
Для решения уравнения устойчивости используем метод деления отрезка пополам. Начальный интервал делим на 2 равные части и вычисляем значение определителя в точке.
Сокращаем на EJ
Все вычисления сводим в таблицу 1.
Таблица 1
|
ν |
φ1(1,225ν) |
φ2(ν) |
r11 |
r12=r12 |
r22 |
D(ν) |
|
1,28 |
0,8227 |
0,9442 |
1,267 |
0,286 |
1,024 |
1,216 |
|
0,64 |
0,9587 |
0,9863 |
1,316 |
0,286 |
1,044 |
1,292 |
|
Из тенденции видно, что значение D(ν) увеличивается, значит для получения D(ν) ≈0 необходимо параметр ν увеличивать |
||||||
|
2,56 |
0,0017 |
0,7597 |
0,972 |
0,286 |
0,936 |
0,828 |
|
3,20 |
-1,7216 |
0,5997 |
0,351 |
0,286 |
0,859 |
0,220 |
|
3,84 |
7,8186 |
0,3676 |
3,786 |
0,286 |
0,747 |
2,748 |
|
3,52 |
-7,4210 |
0,4949 |
-1,701 |
0,286 |
0,809 |
-1,457 |
|
3,36 |
-3,1916 |
0,5498 |
-0,178 |
0,286 |
0,835 |
-0,231 |
|
3,28 |
-2,3079 |
0,5753 |
0,140 |
0,286 |
0,847 |
0,037 |
|
3,29 |
-2,3798 |
0,5722 |
0,114 |
0,286 |
0,846 |
0,015 |
|
3,30 |
-2,4546 |
0,5691 |
0,087 |
0,286 |
0,844 |
-0,008≈0 |
По результатам вычислений принимаем νкр=3,30
Определяем значения критических сил:
- для стойки BС
- для стойки ED
Рама будет отвечать требованиям устойчивости, если
и
где КУ – коэффициент запаса на устойчивость (берется согласно требованиям нормативно-технической документации).
Определяем коэффициенты привидения длин стержней:
Задача №2
Динамический расчет плоской системы
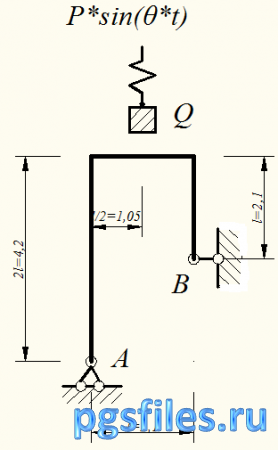
Для плоской рамы (рис. 9) требуется
А. определить круговые частоты свободных вертикальных и горизонтальных колебаний, приняв раму как систему с двумя степенями свободы (собственный вес системы не учитывается);
Б. построить эпюру изгибающих моментов с учетом динамического действия силы Р
Исходные данные:
Ɩ=2,1м;
Q=21кН; EJ=22000кН*м2;
Р=1,5кН; Номер схемы-№4
Система изображенная на рис. 9 имеет две степени свободы. Чтобы определить круговую частоту собственных вертикальных и горизонтальных колебаний, запишем «вековое» уравнение:
[i]
где -единичные перемещения по направлению возможных колебаний массы.
Для определения единичных перемещений строим эпюры М1 и М2. Рассмотрим сначала действие единичной силы, направленной по вертикали, а затем по горизонтали, действующей в точке приложения силы Р
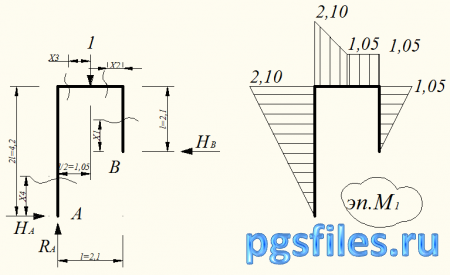
Эпюра М1
Определим опорные реакции:
Определим изгибающие моменты по сечениям рамы, разделив ее на 4 участка
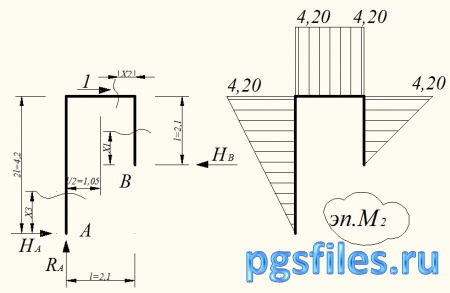
Эпюра М2
Определим опорные реакции:
Определим изгибающие моменты по сечениям рамы, разделив ее на 2 участка
Рис. 11
Вычислим единичные перемещения, используя способ Верещагина:
Обозначая получаем
Решая уравнение получаем корни:
Х1=84,166
Х2=1,691
Вычислим частоты собственных колебаний
Частота изменения вибрационной нагрузки принимается равной половине низшей частоты собственных колебаний системы:
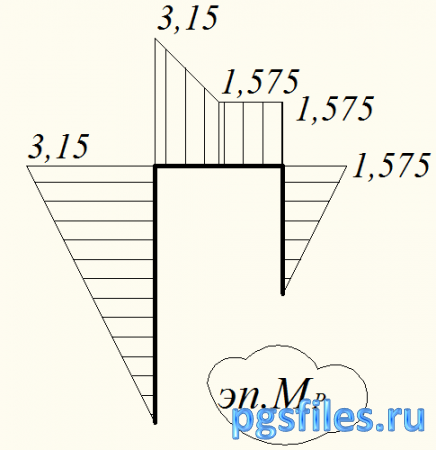
Для построения эпюры изгибающих моментов с учетом статического действия нагрузки воспользуемся эпюрой М1, тогда МР=М1*Р
Рис. 12
Вычислим коэффициенты системы уравнений для определения инерционных сил:
Решаем систему уравнений:
Амплитудные значения сил инерции равны:
I1=0,068кН
I2=-0,161кН
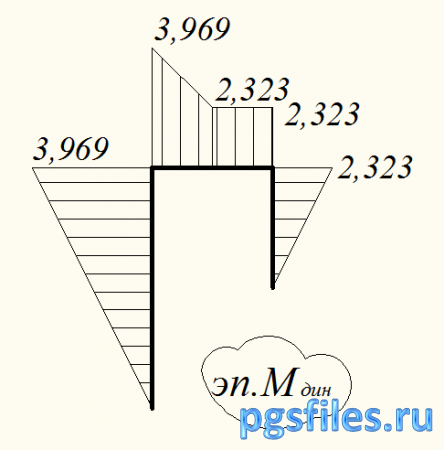
Строим эпюру динамических моментов Мдин: (рис. 13)
Рис. 13
Скачать:





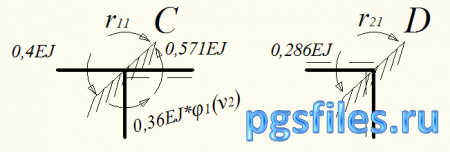
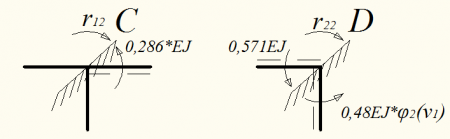
 Юзеры
Юзеры Гости
Гости
 Боты
Боты Всего на сайте
Всего на сайте Администраторов: 1
Администраторов: 1
 Модераторов: 3
Модераторов: 3
 Проектировщиков: 2
Проектировщиков: 2
 Проверенных: 12933
Проверенных: 12933
 Сегодня: 9
Сегодня: 9
